Prisoner’s Dilemma

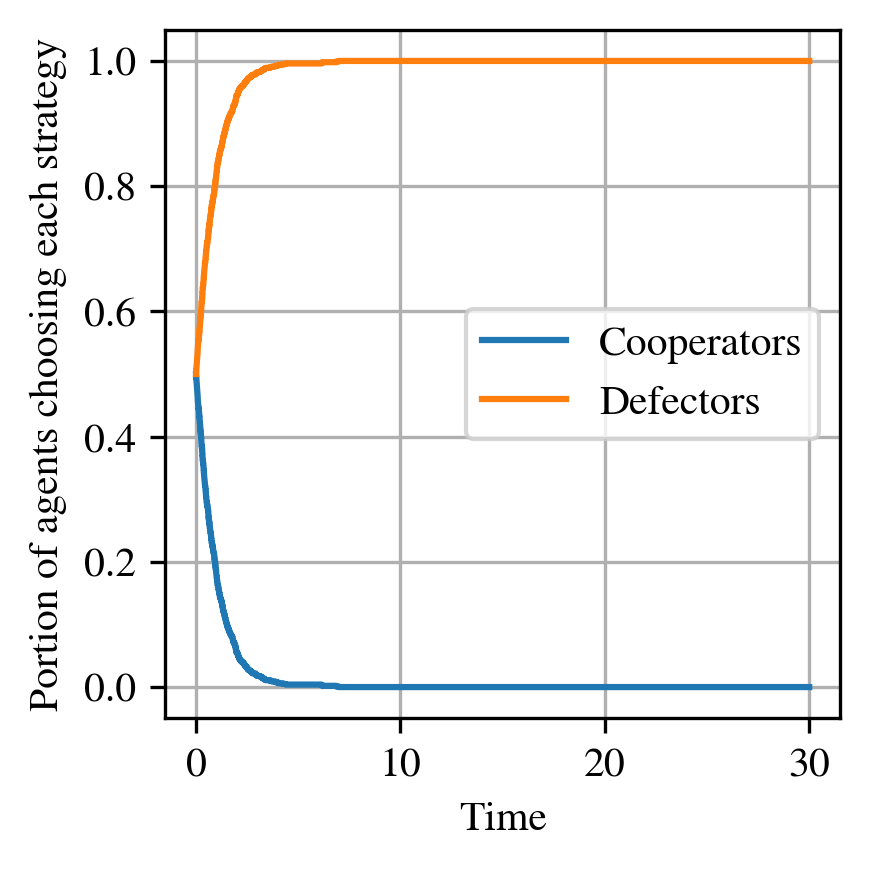
This example models a population of agents repeatedly choosing between two strategies: cooperate or defect, as in the classic Prisoner’s Dilemma game.

It demonstrates how revision dynamics can drive the population toward defection, even when mutual cooperation would be socially optimal.

import numpy as np
import matplotlib.pyplot as plt
from popgames import (
    SinglePopulationGame,
    PayoffMechanism,
    PoissonRevisionProcess,
    Simulator,
)
from popgames.revision_protocol import Softmax

T, R, P, S = 3, 2, 1, 0 # Prisoner's dilemma parameters
                        # s.t. T > R > P > S
                        # https://en.wikipedia.org/wiki/Prisoner%27s_dilemma
def fitness_function(x):
    return np.dot(
        np.array([[R, S], [T, P]]),
        x
    )

population_game = SinglePopulationGame(
    num_strategies=2,
    fitness_function=fitness_function,
)

payoff_mechanism = PayoffMechanism(
    h_map=fitness_function,
    n=2,
)

revision_process = PoissonRevisionProcess(
    Poisson_clock_rate=1,
    revision_protocol=Softmax(0.1),
)

sim = Simulator(
    population_game=population_game,
    payoff_mechanism=payoff_mechanism,
    revision_processes=revision_process,
    num_agents=1000
)

x0 = np.array([0.5, 0.5]).reshape(2, 1)
sim.reset(x0=x0)
out = sim.run(T_sim=30)

plt.figure(figsize=(3, 3))
plt.plot(out.t, out.x[0, :], label='Cooperators')
plt.plot(out.t, out.x[1, :], label='Defectors')
plt.xlabel('Time')
plt.ylabel('Portion of agents choosing each strategy')
plt.legend()
plt.grid()
plt.tight_layout()
plt.show()